Dynamical times and mass accretion rates

Mass accretion rates (MARs) in SPARTA follow the definition of Diemer 2017,

\[\Gamma(t) = \frac{\log[M(t)] - \log[M(t - t_{\rm dyn})]}{\log[a(t)] - \log[a(t - t_{\rm dyn})]}\]

where \(t_{\rm dyn}\) is the dynamical time and the mass is typically defined as \(M_{\rm 200m}\) (though this does not always have to be the case). The dynamical time is based on the typical velocity of a halo,

\[v_{\Delta} \equiv \sqrt{\frac{G M_{\Delta}}{R_{\Delta}}} \,.\]

We use the crossing time such that

\[t_{\rm dyn} \equiv t_{\rm cross} = \frac{2 R_{\Delta}}{v_{\Delta}} \,.\]

This time should roughly describe the time it takes a gravitational tracer to cross a halo. This time is independent of halo mass (as long as spherical overdensity masses are used) and almost independent of cosmology (here shown for \(\Delta_{\rm 200m}\)):

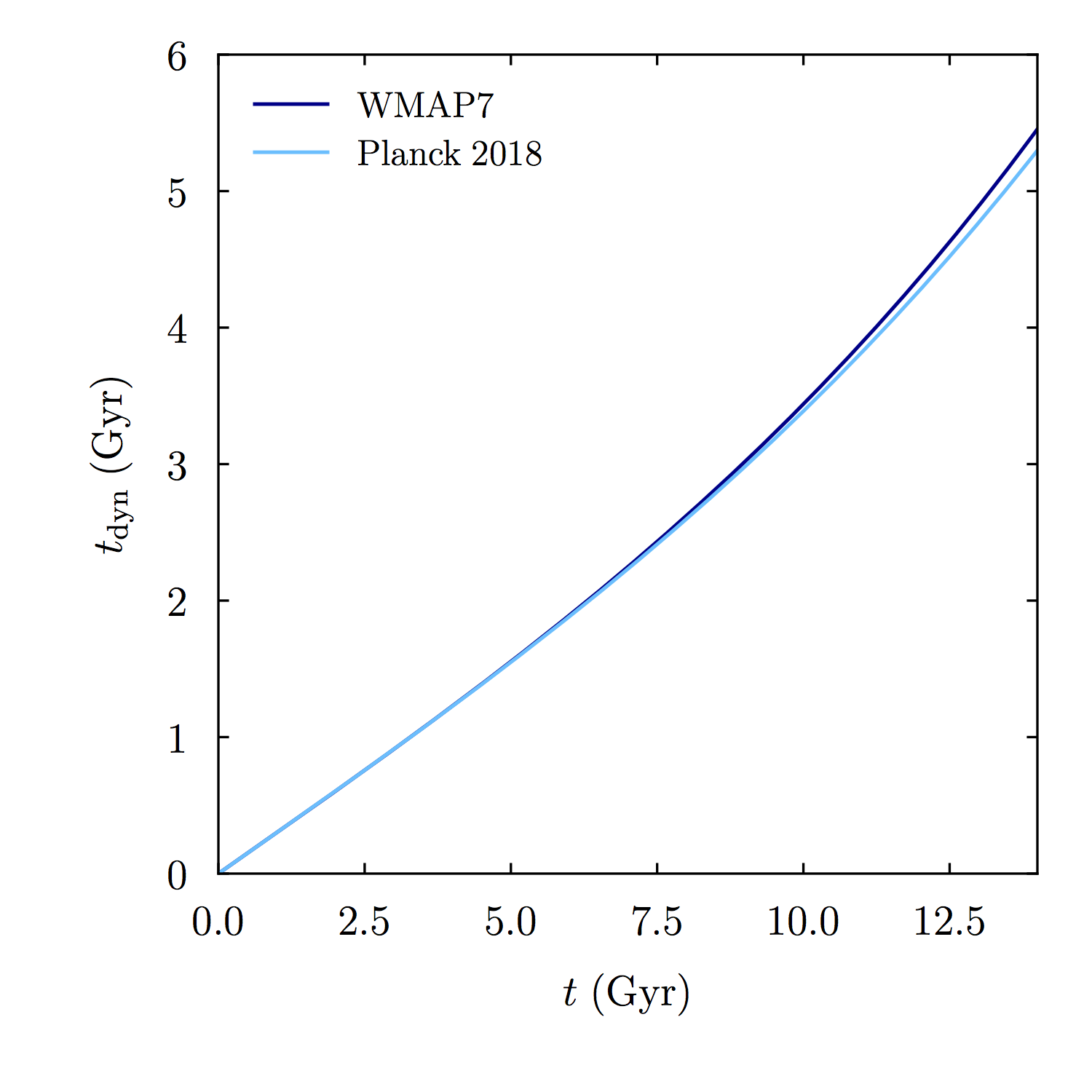
We note that this definition is by no means unique. Most notably, it does not quite correspond to the definition used by Peter Behroozi’s consistent-trees code because

• the definition of dynamical time differs by a factor of two, though this difference can be avoided by using the 2Tdyn accretion rate

• the dynamical time is based on \(\Delta_{\rm vir}\) rather than \(\Delta_{\rm 200m}\), meaning the accretion rate is measured over a slightly different time interval (which makes a surprisingly large difference for a number of halos)

• the mass history is interpolated, whereas the nearest snapshot is taken in SPARTA

• the bound-particle mass is used (though that is very similar to the total SO mass for almost all isolated halos).

For these reasons, one should not expect the two accretion rates to agree quantitatively.