MORIA halo catalogs and merger trees

This document describes the various types of MORIA output files, focusing on the native HDF5 format. As an example, we consider the publicly available catalogs for the Erebos simulations in detail.

Catalog, tree, and original formats

MORIA can output both catalog files (containing all halos at a given snapshot) and tree files (containing halos at all snapshots ordered as halo histories). Moreover, the catalog files can be output in MORIA’s native HDF5 format as well as the original format of the halo finder. See Python for MORIA for convenient routines to read MORIA files.

HDF5 vs. original catalog format

If the output_original parameter is set, MORIA outputs the catalogs in a format as close to the input halo catalogs as possible. For ROCKSTAR catalogs, this means that fields are appended to the header, to the comments, and to each line. These fields are almost exactly identical to those written to the hdf5 output files, with the exception of coordinates and velocities which are omitted (because they are almost always identical to the catalog). However, a given original format may or may not contain all the information in the HDF5 file. For example, configuration parameters are not written to a ROCKSTAR output file. Another important exception are ghosts, i.e., halos that were not part of the original catalog. Even if they are included in MORIA, they are not written to catalogs in the original format.

Note

It is strongly recommended to use the HDF5 output format rather than the original catalog format because certain fields may be omitted, because the accuracy is limited to a certain number of digits (though they are conservatively chosen), because HDF5 leads to smaller file sizes, and because loading HDF5 files is typically much faster than loading text files. Furthermore, MORIA’s tree format is basically identical to the catalog format, and trees cannot be written in the original format.

Catalog vs. tree files

The catalog and tree formats are designed to be as similar as possible. Their only real difference is the ordering of the information, that is, the dimensionality of the datasets. This documentation applies to both formats, we point out differences where appropriate.

The MORIA tree format contains the same datasets as the catalog format, but combines all snapshots into one file. The dimensions of each dataset are n_snapshots by n_halos, where n_halos is the number of halos that are output at ANY snapshot (according to the mass threshold). For example, if a cut on M200m of 200 particles is imposed, halos are output into the tree if they reach 200 particles at any point during their history. In that case, however, their entire history is output, meaning that not all halos fulfill the cut at any given snapshot.

Note that this format differs from other halo finder formats, where halos are output only at those snapshots where they were alive. The advantage of the MORIA format is that it makes it easier to make cuts such as “all snapshots of one halo” or “all halos at one snapshot” (which become simple array indexing operations). The downside is that the datasets contain a significant fraction of zeros. This does not influence the file size much due to compression (see Configuring MORIA). To easily identify and cut out zero epochs, tree files contain an extra dataset called mask_alive, which is True for all epochs and halos where the halo existed, and False otherwise. A second mask, mask_cut, is True only if the halo was output into the corresponding catalog file, that is, if it passed the cut imposed (see Configuring MORIA). Using these masks, it is easy to reconstruct the contents of the catalog files from the tree (and the MORIA loading function can automatically take them into account, see Python for MORIA).

Ghost halos may or may not be part of the catalog files depending on the cut definition. If that is a catalog-based definition, e.g., M200m_peak_cat or Vmax_cat, then ghosts cannot fulfill the requirement and will always be excluded from the catalog files. They will be part of the tree files though, and can be loaded by not applying the cut mask in the load function. For most use cases, ghosts should not be part of the halo sample anyway.

Tree ordering and progenitor/descendant relations

There are a number of ways to format merger tree files, for example breadth first (all halos at a snapshot, then all its subhalos at this snapshot and so on) or depth first (the history of the first halo, the history of its second-largest progenitor and so on). In MORIA, the tree format is somewhat different from conventional formats in that it is intrinsically 2+n dimensional, where the first two dimensions are the number of snapshots and the number of halos. Each field is represented as a dataset with those dimensions, plus possibly additional dimensions (such as 3 for coordinates).

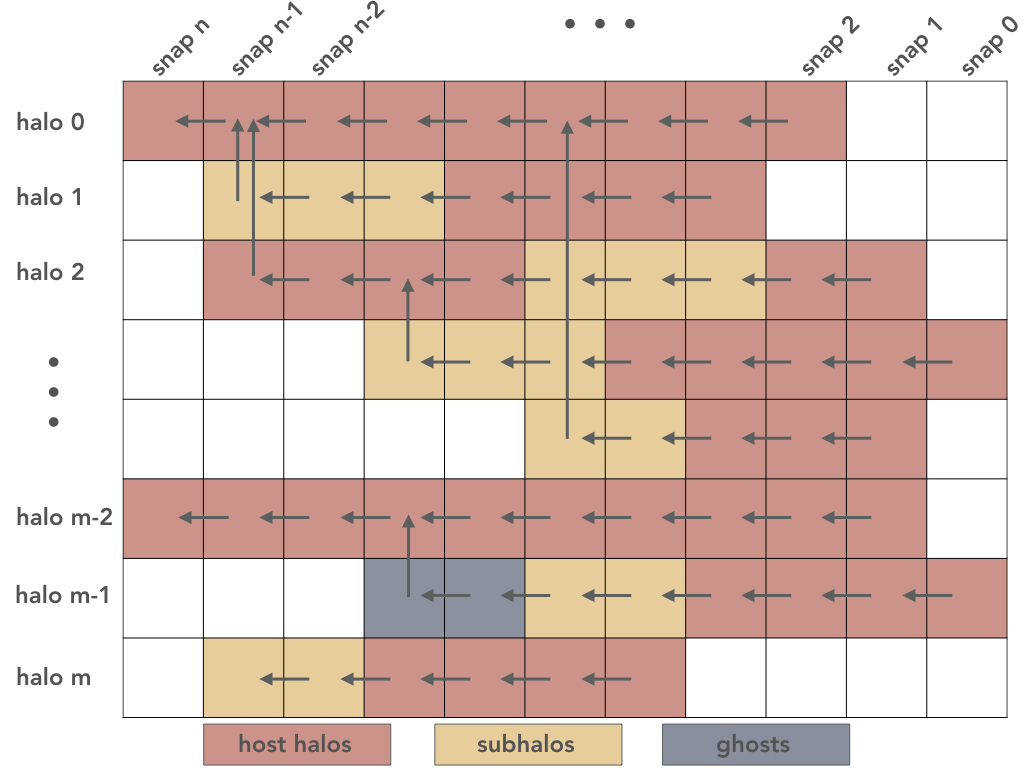
In the above schematic, white fields indicate times where a halo did not exist according to the input halo catalog. Such a format may seem wasteful, but thanks to HDF5 compression there is almost no penalty for large, empty regions. The advantage is that it is now easy to select all halos at a given snapshot, as well as the histories of particular halos.

The arrows indicate progenitor-descendant relations. The fields in each halo correspond to its most massive progenitor branch. When a halo ends, it merges into another halo, indicated by vertical arrows. In the bottom row, a halo ends without merging; in that case, the halo into which it merged is not included in the tree file because it did not meet the output criterion imposed by the user.

The trees are ordered as follows. We consider a halo a “tree root” if it is still alive at the final snapshot, and if it is a host halo. We sort the roots by their mass, that is, the highest value of M200m attained along its history. Behind each root we list its subhalos that survive until the final snapshot. After that, we list the halos that merged into it at snapshot n-1, again sorted by their peak mass, and so on for all snapshots going back to the beginning of the simulation.

If the halo that a halo merged into is not present in the tree (because it did not reach the threshold imposed by the user), we try to find that halo’s “merge parent” and assign the original halo to its tree, and so on. If this procedure does not yield a tree root that is being output, we designate the original halo as a root (bottom row in the schematic). As a result, the vast majority of root halos should be host halos and live to the final snapshot, but there can be exceptions.

The descendant relations are encoded into MORIA tree files in two ways: first, the descendant_id field gives the ID of the descendant halo in the next snapshot, regardless of whether it is included in the tree file (it almost always is, since halos typically merge into larger halos). Second, the descendant_index field gives the index of the descendant in the tree file (between 0 and m-1 in the schematic above). For most of a halo’s life, the descendant index is simply the index of the halo itself.

In the rare case where the halo into which a halo merged was not output, the descendant index is set according to the ordering procedure above, meaning it is set to the “next-higher” halo into which a halo merged, if such a halo exists. If no such tree could be found, the index is -1; it also takes on this value at times when the halo was not alive. At the final snapshot, all descendant IDs and indices are -1; they can differ from the input catalogs if SPARTA was not run until the final snapshot of the simulation (in which case the halos would have descendants at a later snapshot, but they are not included in SPARTA/MORIA).

Ghosts, if included in MORIA, are treated exactly like subhalos. By construction, they merge into the halo which they were a subhalo of during their final snapshot.

Configuration groups

The following sections discuss the various groups and datasets in an HDF5 MORIA file. The tree format is very similar (except for the extra dimension of the datasets), so almost all fields discussed below apply to both catalogs and trees.

The config, simulation, and snapshot attributes

As in a SPARTA output file, the MORIA file contains a config and a simulation group. The former contains an attribute for each configuration parameter (see list above), as well a copy of the entire SPARTA configuration including compiled and run-time parameters.

The simulation group contains similar fields as the corresponding group in a SPARTA file (see The SPARTA HDF5 output format), as well as the additional cosmological parameters passed to MORIA.

The snapshot group (catalogs only)

The snapshot group contains information about the particular snapshot this catalog file refers to. Since trees contain all snapshots, this information is not included in tree files (but it is contained in their config groups):

Field	Type	Explanation
idx	int	The index of the snapshot relative to all snapshots of the simulation
a	float	Scale factor
z	float	Redshift
t	float	Time since Big Bang (Gyr)
rho200m	float	200 times the mean density of the universe
idx_tdyn	int	The index of the snapshot one dynamical time before this snapshot
a_tdyn	float	Scale factor of the snapshot one dynamical time before this snapshot
z_tdyn	float	Redshift of the snapshot one dynamical time before this snapshot
t_tdyn	float	Time since Big Bang (Gyr) one dynamical time before this snapshot
rho200m_tdyn	float	200 times the mean density one dynamical time before this snapshot

See Dynamical times and mass accretion rates for details on how the dynamical time is computed.

Complete list of catalog/tree fields in Erebos catalogs

The following table lists all fields in the Erebos catalogs and trees. The “from” column indicates which of the codes involved calculated a certain field, namely:

• R: Rockstar (halo finder)

• C: Consistent-trees (merger tree construction)

• S: SPARTA

• M: MORIA

In certain cases, the names of fields may contain characters that are not allowed in HDF5 datasets, such as slashes. Those characters are omitted from the names of those datasets. Note that no unit conversions or checks are performed for catalog fields, meaning that the fields appear in a mixture of Rockstar and SPARTA units as indicated in the table. However, the units of the radius definitions are converted by MORIA. For clarity, all length units carry a p or c prefix indicating physical or comoving units. See also Unit system for details on the SPARTA unit system.

All dynamical times in the explanations below are defined in the SPARTA way, that is, as crossing times (two radii over the circular velocity). Rockstar defines the dynamical time as half that time.

Field	Type	Units	From	Explanation
— — — IDs, halo status, and organization — — —
id	int64	–	C,S	Halo ID from the original catalogs (except ghosts, where the ID is determined by SPARTA)
num_prog	int32	–	C	Number of progenitors
descendant_id	int64	–	C,S	ID of the halo at the next snapshot, or of the halo it merged into if it is ending (tree only)
descendant_index	int32	–	M	Tree index of descendant; same as current halo unless merging (tree only)
phantom	int32	–	C	Non-zero if halo was missing in Rockstar and interpolated by Consistent-Trees
mask_alive	int8	–	M	True if there is an alive halo at this index and snapshot (tree only)
mask_cut	int8	–	M	True if halo is part of catalog as well as tree (if it passed the mass threshold, tree only)
status_sparta	int8	–	S	Status of this halo in SPARTA at this snapshot (host/sub/ghost etc, see below)
— — — Radius and mass definitions (at the current time) — — —
R200m_all_spa_internal	float	\({\rm pkpc}/h\)	S	Internally used \(R_{\rm 200m}\) in SPARTA (\(R_{\rm 200m,all}\) for hosts, \(R_{\rm 200m,tcr}\) for subhalos)
M200m_all_spa_internal	float	\(M_{\odot}/h\)	S	Internally used \(M_{\rm 200m}\) in SPARTA (\(M_{\rm 200m,all}\) for hosts, \(M_{\rm 200m,tcr}\) for subhalos)
nu200m_internal	float	–	M	Peak height corresponding to internal \(M_{\rm 200m}\) or bound mass if \(M_{\rm 200m,all}\) > \(2 M_{\rm 200m,bnd}\)
R200m_bnd_cat	float	\({\rm pkpc}/h\)	R	\(R_{\rm 200m}\) computed from bound particles
M200m_bnd_cat	float	\(M_{\odot}/h\)	R	\(M_{\rm 200m}\) computed from bound particles
Rvir_bnd_cat	float	\({\rm pkpc}/h\)	R	\(R_{\rm vir}\) computed from bound particles
Mvir_bnd_cat	float	\(M_{\odot}/h\)	R	\(M_{\rm vir}\) computed from bound particles
R200c_bnd_cat	float	\({\rm pkpc}/h\)	R	\(R_{\rm 200c}\) computed from bound particles
M200c_bnd_cat	float	\(M_{\odot}/h\)	R	\(M_{\rm 200c}\) computed from bound particles
R500c_bnd_cat	float	\({\rm pkpc}/h\)	R	\(R_{\rm 500c}\) computed from bound particles
M500c_bnd_cat	float	\(M_{\odot}/h\)	R	\(M_{\rm 500c}\) computed from bound particles
R200m_all_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 200m}\) computed from all particles
status_moria_hps_R200m_all_spa	int8	–	M	Status of R200m_all_spa (see below)
M200m_all_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 200m}\) computed from all particles
status_moria_hps_M200m_all_spa	int8	–	M	Status of M200m_all_spa (see below)
Rvir_all_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm vir}\) computed from all particles
status_moria_hps_Rvir_all_spa	int8	–	M	Status of Rvir_all_spa (see below)
Mvir_all_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm vir}\) computed from all particles
status_moria_hps_Mvir_all_spa	int8	–	M	Status of Mvir_all_spa (see below)
R200c_all_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 200c}\) computed from all particles
status_moria_hps_R200c_all_spa	int8	–	M	Status of R200c_all_spa (see below)
M200c_all_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 200c}\) computed from all particles
status_moria_hps_M200c_all_spa	int8	–	M	Status of M200c_all_spa (see below)
R500c_all_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 500c}\) computed from all particles
status_moria_hps_R500c_all_spa	int8	–	M	Status of R500c_all_spa (see below)
M500c_all_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 500c}\) computed from all particles
status_moria_hps_M500c_all_spa	int8	–	M	Status of M500c_all_spa (see below)
R200m_tcr_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 200m}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_R200m_tcr_spa	int8	–	M	Status of R200m_tcr_spa (see below)
M200m_tcr_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 200m}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_M200m_tcr_spa	int8	–	M	Status of M200m_tcr_spa (see below)
Rvir_tcr_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm vir}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_Rvir_tcr_spa	int8	–	M	Status of Rvir_tcr_spa (see below)
Mvir_tcr_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm vir}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_Mvir_tcr_spa	int8	–	M	Status of Mvir_tcr_spa (see below)
R200c_tcr_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 200c}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_R200c_tcr_spa	int8	–	M	Status of R200c_tcr_spa (see below)
M200c_tcr_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 200c}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_M200c_tcr_spa	int8	–	M	Status of M200c_tcr_spa (see below)
R500c_tcr_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 500c}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_R500c_tcr_spa	int8	–	M	Status of R500c_tcr_spa (see below)
M500c_tcr_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 500c}\) computed from tracked subhalo particles (all-particle mass for hosts)
status_moria_hps_M500c_tcr_spa	int8	–	M	Status of M500c_tcr_spa (see below)
R200m_orb_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 200m}\) computed from orbiting particles
status_moria_hps_R200m_orb_spa	int8	–	M	Status of R200m_orb_spa (see below)
M200m_orb_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 200m}\) computed from orbiting particles
status_moria_hps_M200m_orb_spa	int8	–	M	Status of M200m_orb_spa (see below)
Rvir_orb_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm vir}\) computed from orbiting particles
status_moria_hps_Rvir_orb_spa	int8	–	M	Status of Rvir_orb_spa (see below)
Mvir_orb_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm vir}\) computed from orbiting particles
status_moria_hps_Mvir_orb_spa	int8	–	M	Status of Mvir_orb_spa (see below)
R200c_orb_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 200c}\) computed from orbiting particles
status_moria_hps_R200c_orb_spa	int8	–	M	Status of R200c_orb_spa (see below)
M200c_orb_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 200c}\) computed from orbiting particles
status_moria_hps_M200c_orb_spa	int8	–	M	Status of M200c_orb_spa (see below)
R500c_orb_spa	float	\({\rm pkpc}/h\)	S	\(R_{\rm 500c}\) computed from orbiting particles
status_moria_hps_R500c_orb_spa	int8	–	M	Status of R500c_orb_spa (see below)
M500c_orb_spa	float	\(M_{\odot}/h\)	S	\(M_{\rm 500c}\) computed from orbiting particles
status_moria_hps_M500c_orb_spa	int8	–	M	Status of M500c_orb_spa (see below)
Morb-all_spa	float	\(M_{\odot}/h\)	S	Mass of all particles that have ever orbited in halo (had a pericenter)
status_moria_hps_Morb-all_spa	int8	–	M	Status of Morb-all_spa (see below)
Rorb-p50_spa	float	\({\rm pkpc}/h\)	S	Radius that includes 50% of orbiting particles
status_moria_hps_Rorb-p50_spa	int8	–	M	Status of Rorb-p50_spa (see below)
Morb-p50_spa	float	\(M_{\odot}/h\)	S	Mass of 50% of orbiting particles
status_moria_hps_Morb-p50_spa	int8	–	M	Status of Morb-p50_spa (see below)
Rorb-p75_spa	float	\({\rm pkpc}/h\)	S	Radius that includes 75% of orbiting particles
status_moria_hps_Rorb-p75_spa	int8	–	M	Status of Rorb-p75_spa (see below)
Morb-p75_spa	float	\(M_{\odot}/h\)	S	Mass of 75% of orbiting particles
status_moria_hps_Morb-p75_spa	int8	–	M	Status of Morb-p75_spa (see below)
Rorb-p90_spa	float	\({\rm pkpc}/h\)	S	Radius that includes 90% of orbiting particles
status_moria_hps_Rorb-p90_spa	int8	–	M	Status of Rorb-p90_spa (see below)
Morb-p90_spa	float	\(M_{\odot}/h\)	S	Mass of 90% of orbiting particles
status_moria_hps_Morb-p90_spa	int8	–	M	Status of Morb-p90_spa (see below)
Rorb-p99_spa	float	\({\rm pkpc}/h\)	S	Radius that includes 99% of orbiting particles
status_moria_hps_Rorb-p99_spa	int8	–	M	Status of Rorb-p99_spa (see below)
Morb-p99_spa	float	\(M_{\odot}/h\)	S	Mass of 99% of orbiting particles
status_moria_hps_Morb-p99_spa	int8	–	M	Status of Morb-p99_spa (see below)
status_sparta_rsp	int8	–	S	Status of Rsp analysis in SPARTA (see below)
status_moria_rsp	int8	–	M	Status of Rsp values in MORIA (see below)
Rsp-apr-mn	float	\({\rm pkpc}/h\)	S	\(R_{\rm sp,mn}\), the splashback radius from mean of particle apocenters
Msp-apr-mn	float	\(M_{\odot}/h\)	S	\(M_{\rm sp,mn}\), the splashback mass from mean of particle apocenters
Rsp-apr-p50	float	\({\rm pkpc}/h\)	S	\(R_{\rm sp,50\%}\), the splashback radius from the 50th percentile of particle apocenters
Msp-apr-p50	float	\(M_{\odot}/h\)	S	\(M_{\rm sp,50\%}\), the splashback mass from the 50th percentile of particle apocenters
Rsp-apr-p70	float	\({\rm pkpc}/h\)	S	\(R_{\rm sp,70\%}\), the splashback radius from the 70th percentile of particle apocenters
Msp-apr-p70	float	\(M_{\odot}/h\)	S	\(M_{\rm sp,70\%}\), the splashback mass from the 70th percentile of particle apocenters
Rsp-apr-p75	float	\({\rm pkpc}/h\)	S	\(R_{\rm sp,75\%}\), the splashback radius from the 75th percentile of particle apocenters
Msp-apr-p75	float	\(M_{\odot}/h\)	S	\(M_{\rm sp,75\%}\), the splashback mass from the 75th percentile of particle apocenters
Rsp-apr-p80	float	\({\rm pkpc}/h\)	S	\(R_{\rm sp,80\%}\), the splashback radius from the 80th percentile of particle apocenters
Msp-apr-p80	float	\(M_{\odot}/h\)	S	\(M_{\rm sp,80\%}\), the splashback mass from the 80th percentile of particle apocenters
Rsp-apr-p85	float	\({\rm pkpc}/h\)	S	\(R_{\rm sp,85\%}\), the splashback radius from the 85th percentile of particle apocenters
Msp-apr-p85	float	\(M_{\odot}/h\)	S	\(M_{\rm sp,85\%}\), the splashback mass from the 85th percentile of particle apocenters
Rsp-apr-p90	float	\({\rm pkpc}/h\)	S	\(R_{\rm sp,90\%}\), the splashback radius from the 90th percentile of particle apocenters
Msp-apr-p90	float	\(M_{\odot}/h\)	S	\(M_{\rm sp,90\%}\), the splashback mass from the 90th percentile of particle apocenters
— — — Subhalo relations — — —
parent_id_cat	int64	–	C	Parent ID according to original catalog, -1 for hosts; equivalent to “upid” (most massive host)
parent_id_R200m_bnd_cat	int64	–	M	Parent ID in R200m_bnd_cat def. or -1 for hosts
parent_id_Rvir_bnd_cat	int64	–	M	Parent ID in Rvir_bnd_cat def. or -1 for hosts
parent_id_R200c_bnd_cat	int64	–	M	Parent ID in R200c_bnd_cat def. or -1 for hosts
parent_id_R500c_bnd_cat	int64	–	M	Parent ID in R500c_bnd_cat def. or -1 for hosts
parent_id_R200m_all_spa	int64	–	M	Parent ID in R200m_all_spa def. or -1 for hosts
parent_id_Rvir_all_spa	int64	–	M	Parent ID in Rvir_all_spa def. or -1 for hosts
parent_id_R200c_all_spa	int64	–	M	Parent ID in R200c_all_spa def. or -1 for hosts
parent_id_R500c_all_spa	int64	–	M	Parent ID in R500c_all_spa def. or -1 for hosts
parent_id_R200m_tcr_spa	int64	–	M	Parent ID in R200m_tcr_spa def. or -1 for hosts
parent_id_Rvir_tcr_spa	int64	–	M	Parent ID in Rvir_tcr_spa def. or -1 for hosts
parent_id_R200c_tcr_spa	int64	–	M	Parent ID in R200c_tcr_spa def. or -1 for hosts
parent_id_R500c_tcr_spa	int64	–	M	Parent ID in R500c_tcr_spa def. or -1 for hosts
parent_id_Rsp-apr-mn	int64	–	M	Parent ID in Rsp-apr-mn def. or -1 for hosts
parent_id_Rsp-apr-p50	int64	–	M	Parent ID in Rsp-apr-p50 def. or -1 for hosts
parent_id_Rsp-apr-p70	int64	–	M	Parent ID in Rsp-apr-p70 def. or -1 for hosts
parent_id_Rsp-apr-p75	int64	–	M	Parent ID in Rsp-apr-p75 def. or -1 for hosts
parent_id_Rsp-apr-p80	int64	–	M	Parent ID in Rsp-apr-p80 def. or -1 for hosts
parent_id_Rsp-apr-p85	int64	–	M	Parent ID in Rsp-apr-p85 def. or -1 for hosts
parent_id_Rsp-apr-p90	int64	–	M	Parent ID in Rsp-apr-p90 def. or -1 for hosts
— — — Important times in the halo history — — —
Mpeak_Scale	float	–	C	Scale factor where highest \(M_{\rm 200m,bnd}\) was reached during halo’s history
Halfmass_Scale	float	–	C	Scale factor where most massive progenitor reached half of \(M_{\rm 200m,bnd,peak}\)
First_Acc_Scale	float	–	C	Scale factor where this halo first became a subhalo, if ever
Acc_Scale	float	–	C	Scale factor where subhalo last became a subhalo, if it ever did
scale_of_last_MM	float	–	C	Scale factor where last merger with mass ratio greater than 0.3 occurred, if ever
Time_to_future_merger	float	\({\rm Gyr}\)	C	Time until the halo merges into a larger halo, if ever
Future_merger_MMP_ID	int64	–	C	ID of most massive progenitor into which this halo merges (-1 if it does not exist at this time)
— — — Alternative mass definitions and definitions at different times — — —
vmax	float	\({\rm km}/s\)	R	Maximum circular velocity, \(\sqrt{G M(<r) / r}\)
Macc	float	\(M_{\odot}/h\)	C	\(M_{\rm 200m,bnd}\) at accretion (for subhalos)
Vacc	float	\({\rm km}/s\)	C	\(V_{\rm max}\) at accretion (for subhalos)
M200m_peak_cat	float	\(M_{\odot}/h\)	C	Highest \(M_{\rm 200m,bnd}\) ever attained during the halo’s history
Mpeak	float	\(M_{\odot}/h\)	C	Same as M200m_peak_cat
Vpeak	float	\({\rm km}/s\)	C	Highest \(V_{\rm max}\) ever attained during the halo’s history
Vmax@Mpeak	float	\({\rm km}/s\)	C	\(V_{\rm max}\) at Mpeak_Scale
First_Acc_Mvir	float	\(M_{\odot}/h\)	C	\(M_{\rm vir,bnd}\) when first becoming subhalo (if ever)
First_Acc_Vmax	float	\({\rm km}/s\)	C	\(V_{\rm max}\) when first becoming subhalo (if ever)
— — — Mass accretion rates — — —
acc_rate_200m_dyn	float	–	M	Fiducial accretion rate of \(M_{\rm 200m,all}\) over \(t_{\rm dyn,200m}\), \(\Gamma_{\rm dyn}\)
status_acc_rate	int8	–	M	Status of acc_rate_200m_dyn (see below)
Acc_Rate_1*Tdyn	float	\(M_{\odot} / h / {\rm yr}\)	C	Accretion rate in \(M_{\rm 200m,bnd}\) over 0.5 \(t_{\rm dyn,vir}\)
Acc_Rate_2*Tdyn	float	\(M_{\odot} / h / {\rm yr}\)	C	Accretion rate in \(M_{\rm 200m,bnd}\) over \(t_{\rm dyn,vir}\)
Acc_Rate_Inst	float	\(M_{\odot} / h / {\rm yr}\)	C	Accretion rate in \(M_{\rm 200m,bnd}\) over one snapshot (very noisy)
Acc_Rate_100Myr	float	\(M_{\odot} / h / {\rm yr}\)	C	Accretion rate in \(M_{\rm 200m,bnd}\) over 100 Myr (short compared to \(t_{\rm dyn}\))
Acc_Rate_Mpeak	float	\(M_{\odot} / h / {\rm yr}\)	C	Accretion rate in \(M_{\rm 200m,bnd,peak}\) from \(z\) to \(z + 0.5\)
Log_(VmaxVmax_max(Tdyn;Tmpeak))	float	–	C	\(\log_{10} V_{\rm max}\) divided by \(V_{\rm max}(t - t_{\rm dyn})\) or \(V_{\rm max}(t_{\rm peak})\) (the latter if \(M_{\rm peak}\) happened more than \(0.5 t_{\rm dyn,vir}\) ago)
Acc_Log_Vmax_1*Tdyn	float	–	C	Difference in \(\log_{10} V_{\rm max}\) over 0.5 \(t_{\rm dyn,vir}\)
Acc_Log_Vmax_Inst	float	–	C	Difference in \(\log_{10} V_{\rm max}\) over one snapshot (very noisy)
— — — Other halo properties — — —
x	float[3]	\({\rm cMpc}/h\)	R,S	Position from Rockstar, except for ghosts where computed by SPARTA
v	float[3]	\({\rm km}/s\)	R,S	Peculiar velocity from Rockstar, except for ghosts where computed by SPARTA
Xoff	float	\({\rm ckpc}/h\)	R	Offset of density peak from average particle position
Voff	float	\({\rm km}/s\)	R	Offset of velocity at density peak from average particle velocity
A[x]	float	\({\rm ckpc}/h\)	R	Largest shape ellipsoid axis vector x-component
A[y]	float	\({\rm ckpc}/h\)	R	Largest shape ellipsoid axis vector y-component
A[z]	float	\({\rm ckpc}/h\)	R	Largest shape ellipsoid axis vector z-component
b_to_a	float	–	R	Ratio of second-largest shape ellipsoid axis B to to largest axis A
c_to_a	float	–	R	Ratio of third-largest shape ellipsoid axis C to to largest axis A
A[x](500c)	float	\({\rm ckpc}/h\)	R	Largest shape ellipsoid axis vector x-component, only counting particles within \(R_{\rm 500c,bnd}\)
A[y](500c)	float	\({\rm ckpc}/h\)	R	Largest shape ellipsoid axis vector y-component, only counting particles within \(R_{\rm 500c,bnd}\)
A[z](500c)	float	\({\rm ckpc}/h\)	R	Largest shape ellipsoid axis vector z-component, only counting particles within \(R_{\rm 500c,bnd}\)
b_to_a(500c)	float	–	R	Ratio of second-largest shape ellipsoid axis B to to largest axis A, only counting particles within \(R_{\rm 500c,bnd}\)
c_to_a(500c)	float	–	R	Ratio of third-largest shape ellipsoid axis C to to largest axis A, only counting particles within \(R_{\rm 500c,bnd}\)
Jx	float	\(M_{\odot}{\rm pMpc}\ {\rm km}/h^2 s\)	R	Angular momentum in x-direction
Jy	float	\(M_{\odot}{\rm pMpc}\ {\rm km}/h^2 s\)	R	Angular momentum in y-direction
Jz	float	\(M_{\odot}{\rm pMpc}\ {\rm km}/h^2 s\)	R	Angular momentum in z-direction
rs	float	\({\rm ckpc}/h\)	R	Scale radius from fit to NFW profile
Rs_Klypin	float	\({\rm ckpc}/h\)	R	Scale radius determined from \(V_{\rm max}\) and \(M_{\rm vir}\) assuming an NFW profile
Halfmass_Radius	float	\({\rm ckpc}/h\)	R	Radius that contains half of \(M_{\rm 200m,bnd}\)
Spin	float	–	R	Spin parameter according to Peebles, \(J\sqrt{|E|} / G M_{\rm vir}^{2/5}\)
Spin_Bullock	float	–	R	Spin parameter according to Bullock, \(J / \sqrt{2 G M_{\rm vir}^3 R_{\rm vir}}\)
Tidal_Force	float	–	C	Strongest tidal force from any nearby halo, in dimensionless units of \(R_{\rm halo} / R_{\rm hill}\)
Tidal_ID	int64	–	C	ID of the halo exerting the strongest tidal force listed in Tidal_Force
Tidal_Force_Tdyn	float	–	C	Tidal force averaged over 0.5 \(t_{\rm dyn,vir}\) in units of \(R_{\rm halo} / R_{\rm hill}\)
vrms	float	\({\rm km}/s\)	R	Velocity dispersion of bound particles
T|U|	float	–	R	Ratio of kinetic and potential energies for bound particles in the halo

Branch-specific fields (tree only)

All datasets in the tree file have dimensions of n_snapshots times n_halos, or rather halo histories or “branches.” However, there are also fields that are specified per branch, as in, where there is one value per halo history. For consistency, those fields are output into a group called branch_data. This group contains the following fields (see also documentation of status fields below):

Field	Type	From	Explanation
status_sparta_final	int8	S	The reason why the halo ended according to SPARTA (see status documentation for values)
first_snap	int16	R,M	First snapshot where the halo was alive (where it was first found in the catalog)
last_snap	int16	R,M	Last snapshot where the halo was alive (can be due to disappearance from catalog, ghost ending, or simulation ending)

Status fields

One key design goal of MORIA is to be transparent about how radii, masses, and other quantities were computed. This information is given in a number of status fields whose names all begin with status_*. Their values are implemented in the Python analysis package module for convenience.

SPARTA status

The first field is status_sparta which tells us the status SPARTA returned for the halo at this snapshot. The following values are possible in the Erebos catalogs:

Value	Meaning	Explanation
-2	NOT_FOUND	Halo was not part of SPARTA output (e.g., too few particles)
0	NONE	Halo did not exist at this snapshot
10	HOST	Host halo
20	SUB	Subhalo
21	BECOMING_SUB	Subhalo; became a subhalo in this snap
22	BECOMING_HOST	Subhalo; will become a host in the next snap
23	BECOMING_SUB_HOST	Subhalo; became sub this snap and will be host in the next
24	SWITCHED_HOST	Subhalo; switched host
31	GHOST_SUB	Ghost subhalo
32	GHOST_SWITCHING	Ghost subhalo, changing host

Please see the Halos & Subhalos page for a full listing of possible numerical values and further explanation of their meaning. When testing for host, subhalo, or ghost status, please use the corresponding functions in Python for SPARTA module instead of manually implementing the status codes (because they could change or be amended, in principle).

The host/sub distinction in SPARTA corresponds to the parent_id_cat field. The status values that indicate changes in the status can also be derived from the parent IDs, but are given for convenience. The ghost status can only be evaluated with the status_sparta field.

Final SPARTA status (reason for ending halo history)

Besides the halo status at each snapshot, SPARTA also assigns each halo history a final status value that gives the reason for why the halo ended. Since there is only one such value per history, this status is stored in the branch_data subdirectory in tree files. It is not output into the MORIA catalog fields because it is not specific to one snapshot. The final status can take on the following values:

Value	Meaning	Explanation
-2	NOT_FOUND	Halo was not part of SPARTA output (e.g., too few particles)
50	MERGED	Halo ended in catalog, i.e., merged with another halo
51	GHOST_CENTER	Particles in ghost have become indistinguishable from host center
52	GHOST_TOO_SMALL	Insufficient particles remaining in ghost
53	GHOST_NOT_FOUND	Too few of the ghost’s previous particles were found in new snap
54	GHOST_POSITION	Ghost position could not be reliably determined
60	LAST_SNAP	Halo reached the last snapshot in the simulation
70	NOT_FOUND	Error: halo could not be found in catalog
71	JUMP	Error: halo position jumped unphysically in catalog
72	HOST_ENDED	Error: could not find host during exchange step
73	SEARCH_RADIUS	Error: no sensible particle distribution found (mostly phantoms)

By far the most common statuses are MERGED and LAST_SNAP. If ghosts are included, they will inevitably survive until the last snapshot or end with one of the ghost-specific final statuses. The error codes should essentially never occur, they mostly indicate issues with the input halo catalog or merger tree.

Mass accretion rate status

The status_acc_rate field tells us how MORIA computed the mass accretion rate. Options include:

Value	Status	Explanation	Console hdr
1	SUCCESS	From SPARTA values for snaps at current time and tdyn	OK
2	REDUCED_INTERVAL	Compressed time interval because halo was a sub in the past	rdcd-tdyn
3	MODEL	Guessed from fitting function	model
4	SUB_SUCCESS	At subhalo infall, computed as for SUCCESS	sub-OK
5	SUB_REDUCED_INTERVAL	At subhalo infall, compressed time interval	sub-rdcd
6	SUB_MODEL	At subhalo infall, guessed from fitting function	sub-model
7	SUB_MODEL_NOW	Despite subhalo, had to guess at current epoch	sb-mdl-nw

The console headers are abbreviations output in the console where we list the fractions of halos with each status (see below). The standard (successful) determination of the accretion rate occurs when we find M200m_all at the current time and one dynamical time ago (SUCCESS).

If the halo happened to be a subhalo one dynamical time ago (and then became a host again), we should not use its mass at that previous snapshot. Instead, we go forward in time to find the snapshot when it became a host again (REDUCED_INTERVAL), but only if that time is at least 0.25 dynamical times in the past (to avoid very noisy short-interval measurements). If this mechanism also fails, we use the fitting function of Diemer 2020 (MODEL).

Note

Mass accretion rates estimated with the fitting function do not reflect the real distribution of MARs, but rather their median value (ignoring the sizeable scatter).

For subhalos, the current mass is ill-defined, and the mass accretion rate while a subhalo makes little sense either. Thus, we attempt to compute the MAR at infall, that is, at the last snapshot before the halo became a subhalo. Again, if the halo was a host one dynamical time before that, we use that time (SUB_SUCCESS); if not, we reduce the time interval as for hosts (SUB_REDUCED_INTERVAL). We note that the MARs at infall are not the same as the current MARs, and that the two should not be compared directly. The rates at infall are given mostly for completeness.

If this mechanism fails, we need to evaluate the fitting function again. If we can determine the time of infall of subhalos, we evaluate the model at that time (SUB_MODEL). If not, we have no choice but to evaluate the model at the current time, giving a highly unreliable estimate (SUB_MODEL_NOW). This case should only occur if not all halos are present in a SPARTA output file, meaning the output criteria are poorly matched in MORIA and SPARTA.

In practice, almost all host halos should have successful determinations of the MAR, with the other statuses representing rare edge cases.

Status of splashback analysis

The status_sparta_rsp field tells us whether the splashback radii and masses could be he Rsp analysis that SPARTA returned. The meaning of the codes is documented on the Splashback radius analysis page.

Value	Parameter	Explanation
1	SUCCESS	The analysis succeeded, all output values can be used
2	HALO_NOT_VALID	Halo could not be analyzed at this snapshot, e.g. because too young
5	INSUFFICIENT_EVENTS	There were not enough particle splashback events
6	INSUFFICIENT_WEIGHT	There were enough particle splashback events, but their weight was too low

Based on the SPARTA status, MORIA accepts the values or attempts to improve the completeness. The status_moria_rsp tells us how MORIA processed the splashback radii and masses:

Value	Status	Explanation	Console hdr
1	SPARTA_SUCCESS	Success, the Rsp and Msp values were taken from SPARTA	OK
2	ESTIMATED_MODEL	Guessed Rsp and Msp from fitting function	gs-model
3	ESTIMATED_PAST	Guessed Rsp and Msp from past snapshot	gs-past
4	ESTIMATED_FUTURE	Guessed Rsp and Msp from future snapshot	gs-ftre
5	ESTIMATED_INTERPOLATED	Guessed Rsp and Msp from past and future snaps via interpolation	gs-intrp

The status applies to all Rsp/Msp definitions. The algorithm for determining Rsp and Msp is as follows:

• If there is a SPARTA entry/analysis for this halo, we take the values from that (SPARTA_SUCCESS).

• If Rsp and Msp could not determined by SPARTA, MORIA needs to guess. First, we look for past and future snapshots with valid Rsp/Msp from SPARTA within a dynamical time of the current snapshot. If at least one is found, we use the same Rsp/R200m and Msp/M200m and apply it at the current snapshot (ESTIMATED_PAST or ESTIMATED_FUTURE). If both are found, we interpolate Rsp/R200m and Msp/M200m linearly in time (ESTIMATED_INTERPOLATED).

• If no valid snapshots are found within a dynamical time, we guess Rsp/R200m and Msp/M200m using the fitting function of Diemer 2020 (ESTIMATED_MODEL). We use the real mass accretion rate of the halo if available, or another fitting function if not (see status_acc_rate above).

Status of SO definitions from SPARTA

Unlike the Rsp analysis, the HaloProps analysis returns a status for each definition because they can suffer different fates (for example, an SO threshold may be reached in one definition but not in another). Thus, MORIA returns a status_moria_hps_<def> field for each definition. This field combines the SPARTA status (as listed on the Halo properties analysis page) with any modifications MORIA made:

Value	Status	Explanation	Console hdr
1	SPARTA_SUCCESS	Success, the Rsp and Msp values were taken from SPARTA	OK
2	SO_TOO_SMALL	SO threshold was not reached at center, halo not dense enough	so_small
3	SO_TOO_LARGE	SO threshold was not reached at edge, halo too dense at large r	so_large
4	ORB_ZERO	No orbiting particles were found	oct_zero

Phantoms

Phantoms are halos that were not found by the halo finder at a given snapshot, but that were reconstructed from previous and future snapshots. For example, halos can temporarily disappear while crossing through a larger halo, but not all phantoms are necessarily subhalos. In Rockstar catalogs, the number of phantoms is typically small, much less than a percent, but they cause issues for SPARTA because their positions are not accurate, leading to unphysical density profiles and so on.

Thus, at least when using Rockstar catalogs, it is recommended to add the phantom field to the fields copied from the halo finder output, and to exclude phantoms from analyses of their properties wherever possible.

F.A.Q. about Erebos catalogs/trees

The following questions and answers are somewhat specific to the public Erebos catalogs and merger trees. Many decisions that were made could, in principle, be changed in the configuration parameters.

Which halos are included?

SPARTA considers all halos in the input catalogs. However, only halos that have at least 100 particles within R200m (as defined by SPARTA) at any snapshot are output into the SPARTA files.

In MORIA, a stricter cut of 200 particles was made, but in the peak M200m from bound particles according to Rockstar. This cut avoids halos that might have been assigned an unphysically large M200m due to neighboring halos.

Despite the more conservative cut in MORIA, there is a very small fraction of halos in the MORIA catalogs and trees that were not part of the SPARTA output. This happens in the extremely rare case where a halo never reaches an M200m of 100 particles while it is a host but reaches at least 200 particles according to Rockstar while it is a subhalo. In that case, SPARTA may assign the halo a smaller mass (computed from particle tracking). If that mass remains below 100 particles, the halo never makes the threshold for being output.

How can the SPARTA status and final status be NOT_FOUND?

See the point above – some halos are not part of the SPARTA files, in which case the status output by MORIA is NOT_FOUND.

Known issues

Comoving force softening

In the SPARTA runs, the force softening of the Erebos simulations was erroneously set to a fixed physical length even though the actual force softening is given in comoving units, i.e., evolves with redshift. Specifically, the config parameter sim_force_res_comoving was set to 0 instead of 1. This error has only a very minor impact on SPARTA’s calculations, but the incorrect parameter is part of the SPARTA / MORIA files.